Is it time for the U.S. to go metric?

[U4K61]

The Circle

One measure that does not have a metric equivalent is the 360° circle, which was at one time was to be changed to 100 to go along with the rest of the metric system. The composite number 360 was found to be a special number as it can be divided 22 ways to produce an integer whole number, unlike a prime number, that can be only divided by one or itself.

360/1 = 360, 360/360 = 1
360/2 = 180, 360/180 = 2
360/3 = 120, 360/120 = 3
360/4 = 90, 360/90 = 4
360/5 = 72, 360/72 = 5
360/6 = 60, 360/60 = 6
360/8 = 45, 360/45 = 8
360/9 = 40, 360/40 = 9
360/10 = 36, 360/36 = 10
360/12 = 30, 360/30 = 12
360/18 = 20, 360/20 = 18

360 has Babylonian sexagesimal DNA:
1 talent = 60 mina
1 mina = 60 shekel
Sixtieths - pars minuta prima (minutes)
Sixtieths of sixtieths - pars minute secunda (seconds)

360/3 gives 120 which allows integer multiples of 24fps, 30fps, and 60fps film and video!
Also, dropping 360 for some other number would have left M$ searching for a different name for their RROD game system.

π = C/d
It is the irrational number 3.14159265... that can't be expressed as the integers m/n. It is the ratio of a circle's circumference to its diameter in Euclidean space. Lambert's proof (1761): using the concept of the continued fraction P/Q = a+1/(b+1/(c+1/(d+...))).
π = 3 + (7 + (15 + (1 + (292 + (1 + (1 + (1 + (2 + ...)^-1)^-1)^-1)^-1)^-1)^-1)^-1)^-1


Area = πr²
Rearrangement proof
On way to show πr² is to break up the circle into smaller and smaller equally sized pieces. Using one line (2^0) down the middle to create two halves together equeling the whole. Each half gets broken into two equally sized peices using (2^1) lines, so the number of pieces totals 4 parts. As n approaches infinity (2^n), the pie shaped slices become closer to lines which when laid side by side will form a rectange whose area is L x W.

Onion proof, let b = r, a = 0 and ∫ f(t)dt = F(b) - F(a)
Area(r); = ∫ 2πt dt = [(2π)(t²/2)] = πr²

Triangle proof
A bit like the Onion proof, we begin with concentric circles. By unwrapping them to form straight strips, we create a right angled triangle with r as its height and 2πr as its base. Area = 1/2(base x height) = 1/2(2πr x r) = πr²


Unit Circle, x² + y² = 1² or x² + y² = 1
A unit circle is a circle with a radius of one centered at the origin (0, 0). If we let x=cos and y=sin, then we have the identity (cos(θ))² + (sin(θ))² = 1, and tan = sin/cos. At 0°, cos=1, sin=0 and tan=0; at 45°(π/4), x and y are equal, so y=x; at 90°(π/2), cos=0, sin=1 and tan is undefined.

The radian (rad) is the ratio between the length of an arc and its radius where arc length = radius. The circumfrence of a circle is πd or 2πr which is a one complete revolution or 360°; 2πr ⇔ 360°. When we use the unit circle, r = 1 and so we have 2π1 or 2π. 1 rad = (360°/2π).


Riemann Sphere, C
The Riemann sphere, C, is the unit sphere S = {Z ∈ R3 : |Z| = 1} and we use the x-y plane to represent C. Each point Z ∈ C corresponds to a point Z ∈ S by stereographic projection to the north pole N. C, is the one-point compactification of the complex plane by identifying the limits of all infinitely extending rays from the origin as one single point at infinity. 1/0 = ∞, 1/∞ = 0. A circle that goes through the north pole at infinity is projected as a line on the plane.
z + ∞ = ∞
z ⋅ ∞ = ∞.


Hyperbolic Geometry (Bolyai-Lobachevskian)
The angles of a triangle add to less than a straight angle which is 180° or π. The shortfall is proportional to the area: π - (α + β + γ) = CΔ, where Δ is the area and C is some constant. In the limit as the vertices go to infinity, there are even ideal hyperbolic triangles in which all three angles are 0°.

Glossery

Some Important Formula
Circumference of circle = πd or 2πr
Area of circle = πr²
Volume of cylinder = πr²h
Area of sphere = 4πr²
Volume of sphere = 4/3πr³

Types of Angle
Acute angle < π/2
Right angle = π/2
Obtuse angle > π/2 and < π
Straight angle = π
Reflex angle > π and < 2π
Full angle = 2π

Radian
An angle of one radian subtended from the center of a unit circle produces an arc with arc length 1. A radian cuts out a length of a circle's circumference equal to the radius.
0° = 0, 30° = π/6, 45° = π/4, 60° = π/3, 90° = π/2, 180° = π, 360° = 2π

Steradian (stereos, greek 'solid', radius, Latin 'ray or beam')
The unit of solid angle. Cuts out an area of a sphere equal to radius².
The surface area of a sphere is 4πr².
The surface area of a steradian is r2.

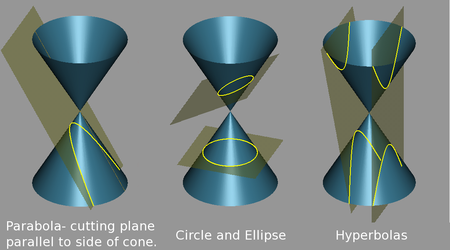
Conic Sections
Circle, x² + y² = r², (x-h)² + (y-k)² = r²
Ellipse, for a > b, Horizontal x²/a² + y²/b² = 1, Vertical x²/b² + y²/a²
Parabola, (y-k)² = 4a(x-h)
Hyperbola, x²/a² - y²/b² = 1




Complex Numbers, z = x + yi.
The complex plane: x-axis is real (R), y-axis (i); i = √-1, the angle between i and x-axis is 90°.
i^0=1 (0°), i^1=i (90°), i^2=-1 (180°), i^3=-i (270°), i^4=1 (360°);
The nth power multiplies its angle by n.
√-25 = √25√-1 = 5i. (3i)(4i) = (3⋅4)(i⋅i) = 12(i^2) = (12)(-1) = -12.

(a + ib) + (c + id) = (a + c) + i(b + d)

(a + ib)(c + id) = ac + ibc + aid + ibid = ac + i(bc + ad) + i^2bd = (ac - bd) + i(bc + ad)
(2 – i)(3 + 4i) = 6 + 8i – 3i – 4i^2 = 10 + 5i

|3 - 2i| = √((3)^2 + (2)^2) = √13 = 3.61 The Distance Formula.


Euclids Postulates
1. A straight line segment can be drawn joining any two points.
2. Any straight line segment can be extended indefinitely in a straight line.
3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
4. All right angles are congruent.
5. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. This postulate is equivalent to what is known as the parallel postulate.

Congruence
1. Two line segments are congruent if they have the same length. But they need not lie at the same angle or position on the plane.
2. Two angles are congruent if they have the same measure. Congruent angles may lie in different orientations or positions.
3. Two circles are congruent if they have the same size. They can overlap.


Set Cardinality
Back to Metric Measurement